Results Reader¶
Basic operations¶
This notebook demonstrates the capabilities of the serpentTools to read
Serpent results files. SERPENT [serpent] produces a result file (i.e.
_res.m), containing general results (e.g. k-eff), metadata (e.g.
title) and homogenized cross-sections. The homogenized cross-section
sets are printed in the results file for all the requested universes.
The ResultsReader is capable of reading this file, and storing the data
inside HomogUniv objects. Each such object has methods and attributes that
should ease the analyses.
Note
The preferred way to read your own output files is with the
serpentTools.read() function. The serpentTools.readDataFile() function is used here
to make it easier to reproduce the examples
>>> import numpy as np
>>> import serpentTools
>>> from serpentTools.settings import rc
>>> resFile = 'InnerAssembly_res.m'
>>> res = serpentTools.readDataFile(resFile)
Metadata¶
metadata is a collective data that describes the problem. These are values
that do not change over burnup and across homogenized universes. The
following data is included: titles, data paths, and other descriptive
data exist on the reader
>>> print(res.metadata['version'])
Serpent 2.1.30
>>> print(res.metadata['decayDataFilePath'])
/nv/hp22/dkotlyar6/data/Codes/DATA/endfb7/sss_endfb7.dec
>>> print(res.metadata['inputFileName'])
InnerAssembly
>>> res.metadata.keys()
dict_keys(['version', 'compileDate', 'debug', 'title', 'confidentialData',
'inputFileName', 'workingDirectory', 'hostname', 'cpuType', 'cpuMhz',
'startDate', 'completeDate', 'pop', 'cycles', 'skip', 'batchInterval',
'srcNormMode', 'seed', 'ufsMode', 'ufsOrder', 'neutronTransportMode',
'photonTransportMode', 'groupConstantGeneration', 'b1Calculation',
'b1BurnupCorrection', 'implicitReactionRates', 'optimizationMode',
'reconstructMicroxs', 'reconstructMacroxs', 'doubleIndexing', 'mgMajorantMode',
'spectrumCollapse', 'mpiTasks', 'ompThreads', 'mpiReproducibility',
'ompReproducibility', 'ompHistoryProfile', 'shareBufArray', 'shareRes2Array',
'xsDataFilePath', 'decayDataFilePath', 'sfyDataFilePath', 'nfyDataFilePath',
'braDataFilePath'])
>>> res.metadata['startDate']
'Sat Apr 28 06:09:54 2018'
>>> res.metadata['pop'], res.metadata['skip'] , res.metadata['cycles']
(5000, 10, 50)
Results Data¶
Results are stored as a function of time/burnup/index and include
integral parameters of the system. Results, such as k-eff, total
flux, and execution times are included in resdata. Some results
include values and uncertainties (e.g. criticality) and some just the
values (e.g. CPU resources).
>>> sorted(res.resdata.keys())[0:5]
['absKeff', 'absKinf', 'actinideActivity', 'actinideDecayHeat', 'actinideIngTox']
Values are presented in similar fashion as if they were read in to Matlab, with one
exception. Serpent currently appends a new row for each burnup step, but also for
each set of homogenized universe. This results in repetition of many quantities
as Serpent loops over group constant data. The ResultsReader understands Serpent
outputs and knows when to append “new” data to avoid repetition.
The structure of the data is otherwise identical to Matlab. For many quantities, the first column contains expected values, and the second column contains relative uncertainties.
>>> res.resdata['absKeff'])
array([[ 1.29160000e+00, 9.00000000e-04],
[ 1.29500000e+00, 9.30000000e-04],
[ 1.29172000e+00, 9.10000000e-04],
[ 1.29172000e+00, 7.80000000e-04],
[ 1.29312000e+00, 6.80000000e-04],
[ 1.29140000e+00, 7.80000000e-04]]
>>> res.resdata['absKeff'][:,0]
array([ 1.2916 , 1.295 , 1.29172, 1.29172, 1.29312, 1.2914 ])
>>> res.resdata['burnup']
array([[ 0. , 0. ],
[ 0.1 , 0.100001],
[ 1. , 1.00001 ],
[ 2. , 2.00001 ],
[ 3. , 3.00003 ],
[ 4. , 4.00004 ]]
>>> res.resdata['burnDays']
[[ 0. ],
[ 1.20048],
[ 12.0048 ],
[ 24.0096 ],
[ 36.0144 ],
[ 48.0192 ]]
Data in the resdata can be obtained
directly by indexing into the reader:
>>> res["burnup"]
array([[ 0. , 0. ],
[ 0.1 , 0.100001],
[ 1. , 1.00001 ],
[ 2. , 2.00001 ],
[ 3. , 3.00003 ],
[ 4. , 4.00004 ]]
>>> res.resdata.get('absKeff'))
array([[ 1.29160000e+00, 9.00000000e-04],
[ 1.29500000e+00, 9.30000000e-04],
[ 1.29172000e+00, 9.10000000e-04],
[ 1.29172000e+00, 7.80000000e-04],
[ 1.29312000e+00, 6.80000000e-04],
[ 1.29140000e+00, 7.80000000e-04]]
Plotting Results Data¶
The ResultsReader has a versatile
plot() method,
used to plot primary time-dependent data from the result file.
One can plot data from one or more quantities against various
metrics of time. Control over axis formatting, legend placement,
and label formatting is easily yielded to the user.
>>> res.plot('absKeff')
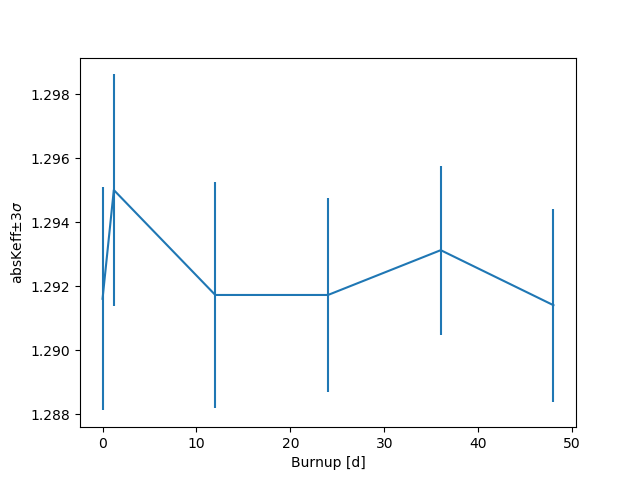
>>> res.plot('burnup', ['absKeff', 'colKeff'])
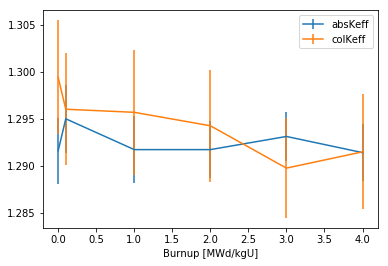
Pass a dictionary of variable: label pairs to set plot labels.
>>> res.plot(
>>> 'burnup', {
>>> 'absKeff': '$k_{eff}^{abs}$',
>>> 'colKeff': '$k_{eff}^{col}$',},
>>> ylabel=r'Criticality $\pm 3\sigma$',
>>> legend='above', ncol=2,
>>> )
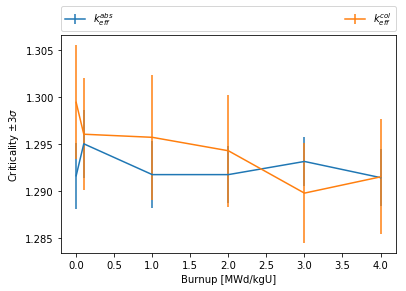
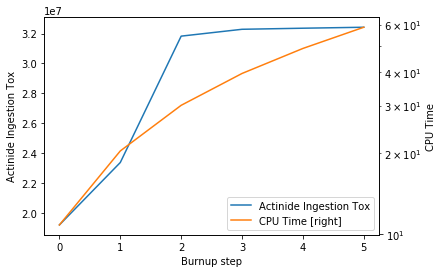
Using the right argument, quantities can be plotted using the
left and right y-axis. Similar formatting options are available.
>>> res.plot(
>>> 'burnStep',
>>> {'actinideIngTox': 'Actinide Ing. Tox'},
>>> right={'totCpuTime': 'CPU Time [right]'},
>>> sigma=0, rightlabel="CPU Time",
>>> # set the yscale to log only of right axis
>>> logy=[False, True],
>>> )
Universe Data¶
Universe data is stored for each state point in the universes dictionary. Keys are
UnivTuple representing ('univ',burnup, burnupIdx, time)
'univ': universe ID (e.g.,'0')burnup: in MWd/kg,burnupIdx: step indextime: in days
and can be indexed by attribute or by position.
>>> for key in sorted(res.universes):
... break
>>> key
UnivTuple(universe='0', burnup=0.0, step=0, days=0.0)
>>> key[0]
'0'
>>> key.burnup == key[1]
True
Results, such as infinite cross-sections, b1-leakage corrected
cross-sections, kinetic parameters, are included in universes.
All the results include values and uncertainties.
>>> res.universes.keys()
dict_keys([
UnivTuple(universe='3101', burnup=0.0, step=0, days=0.0),
UnivTuple(universe='3102', burnup=0.0, step=0, days=0.0),
UnivTuple(universe='0', burnup=0.0, step=0, days=0.0),
UnivTuple(universe='3101', burnup=0.1, step=1, days=1.20048),
UnivTuple(universe='3102', burnup=0.1, step=1, days=1.20048),
...
UnivTuple(universe='3101', burnup=4.0, step=5, days=48.0192),
UnivTuple(universe='3102', burnup=4.0, step=5, days=48.0192),
UnivTuple(universe='0', burnup=4.0, step=5, days=48.0192)])
One can directly index into universes to obtain a specific HomogUniv
object:
>>> print(res.universes['0', 0, 0, 0])
<HomogUniv 0: burnup: 0.00000E+00 MWd/kgU, 0.00000E+00 days>
However, this requires knowledge of all four parameters, which may be difficult.
The getUniv() method retrieves the first universe that matches a set of parameters,
the universe and at least one point in time. While all four identifiers (universe id,
burnup, step, and time) can be provided, the latter three are usually redundant.
>>> univ0 = res.getUniv('0', timeDays=24.0096)
>>> print(univ0)
<HomogUniv 0: burnup: 0.00000E+00 MWd/kgU, 0.00000E+00 days>
>>> univ3101 = res.getUniv('3101', index=3)
>>> print(univ3101)
<HomogUniv 3101: burnup: 2.00000E+00 MWd/kgU, 2.40096E+01 days>
>>> univ3102 = res.getUniv('3102', burnup=0.1)
>>> print(univ3102)
<HomogUniv 3102: burnup: 1.00000E-01 MWd/kgU, 1.20048E+00 days>
Working with homogenized universe data¶
Each state contains the same data fields, which can be obtained by using
the following attributes on the HomogUniv object:
infExp: infinite values, e.g.INF_ABSinfUnc: infinite uncertaintiesb1Exp: b1 (leakage corrected) values, e.g.B1_ABSb1Unc: b1 (leakage corrected) uncertaintiesgc: variables that are not included ininforb1, e.g.BETAgroups: macro energy group structure, MeVmicroGroups: micro energy group structure, MeV
The parser reads all the variables by default. The values are all energy dependent in the order they would appear in the results file:
>>> univ0.infExp.keys()
dict_keys(['infMicroFlx', 'infKinf', 'infFlx', 'infFissFlx', 'infTot',
'infCapt', 'infAbs', 'infFiss', 'infNsf', 'infNubar', 'infKappa', 'infInvv',
'infScatt0', 'infScatt1', 'infScatt2', 'infScatt3', 'infScatt4', 'infScatt5',
'infScatt6', 'infScatt7', 'infScattp0', 'infScattp1', 'infScattp2',
'infScattp3', 'infScattp4', 'infScattp5', 'infScattp6', 'infScattp7',
'infTranspxs', 'infDiffcoef', 'infRabsxs', 'infRemxs', 'infI135Yield',
'infXe135Yield', 'infPm147Yield', 'infPm148Yield', 'infPm148mYield',
'infPm149Yield', 'infSm149Yield', 'infI135MicroAbs', 'infXe135MicroAbs',
'infPm147MicroAbs', 'infPm148MicroAbs', 'infPm148mMicroAbs',
'infPm149MicroAbs', 'infSm149MicroAbs', 'infXe135MacroAbs', 'infSm149MacroAbs',
'infChit', 'infChip', 'infChid', 'infS0', 'infS1', 'infS2', 'infS3', 'infS4',
'infS5', 'infS6', 'infS7', 'infSp0', 'infSp1', 'infSp2', 'infSp3', 'infSp4',
'infSp5', 'infSp6', 'infSp7'])
>>> univ0.infExp['infAbs']
array([ 0.0170306 , 0.0124957 , 0.00777066, 0.00773255, 0.00699608,
0.00410746, 0.00334604, 0.00296948, 0.0030725 , 0.00335412,
0.00403133, 0.00506587, 0.00651475, 0.00737292, 0.00907442,
0.0113446 , 0.0125896 , 0.0164987 , 0.0181642 , 0.0266464 ,
0.0292439 , 0.0315338 , 0.0463069 , 0.0807952 ])
>>> univ0.infExp['infFlx']
array([ 1.10460000e+15, 1.72386000e+16, 7.78465000e+16,
1.70307000e+17, 2.85783000e+17, 4.61226000e+17,
8.04999000e+17, 1.17536000e+18, 1.17488000e+18,
1.26626000e+18, 1.03476000e+18, 7.58885000e+17,
4.95687000e+17, 5.85369000e+17, 2.81921000e+17,
1.16665000e+17, 8.06833000e+16, 2.26450000e+16,
6.51541000e+16, 2.79929000e+16, 8.87468000e+15,
1.70822000e+15, 8.87055000e+14, 6.22266000e+13])
Uncertainties can be obtained in a similar was by using the infUnc field:
>>> univ0.infUnc['infFlx']
array([0.02125, 0.0287 , 0.00901, 0.00721, 0.00441, 0.00434, 0.00448,
0.0007 , 0.00369, 0.00071, 0.00045, 0.00133, 0.00061, 0.00341,
0.00674, 0.00197, 0.00802, 0.00368, 0.00127, 0.00046, 0.02806,
0.0491 , 0.19529, 0.16476])
Serpent also outputs the B1 cross-sections. However, the user must
enable the B1 option by setting the fum card:
http://serpent.vtt.fi/mediawiki/index.php/Input_syntax_manual#set_fum
If this card is not enabled by the user, the B1_ variables will all
be zeros.
>>> univ0.b1Exp.keys()
dict_keys(['b1MicroFlx', 'b1Kinf', 'b1Keff', 'b1B2', 'b1Err', 'b1Flx',
'b1FissFlx', 'b1Tot', 'b1Capt', 'b1Abs', 'b1Fiss', 'b1Nsf', 'b1Nubar',
'b1Kappa', 'b1Invv', 'b1Scatt0', 'b1Scatt1', 'b1Scatt2', 'b1Scatt3',
'b1Scatt4', 'b1Scatt5', 'b1Scatt6', 'b1Scatt7', 'b1Scattp0', 'b1Scattp1',
'b1Scattp2', 'b1Scattp3', 'b1Scattp4', 'b1Scattp5', 'b1Scattp6', 'b1Scattp7',
'b1Transpxs', 'b1Diffcoef', 'b1Rabsxs', 'b1Remxs', 'b1I135Yield',
'b1Xe135Yield', 'b1Pm147Yield', 'b1Pm148Yield', 'b1Pm148mYield',
'b1Pm149Yield', 'b1Sm149Yield', 'b1I135MicroAbs', 'b1Xe135MicroAbs',
'b1Pm147MicroAbs', 'b1Pm148MicroAbs', 'b1Pm148mMicroAbs', 'b1Pm149MicroAbs',
'b1Sm149MicroAbs', 'b1Xe135MacroAbs', 'b1Sm149MacroAbs', 'b1Chit', 'b1Chip',
'b1Chid', 'b1S0', 'b1S1', 'b1S2', 'b1S3', 'b1S4', 'b1S5', 'b1S6', 'b1S7',
'b1Sp0', 'b1Sp1', 'b1Sp2', 'b1Sp3', 'b1Sp4', 'b1Sp5', 'b1Sp6', 'b1Sp7'])
>>> univ3101.b1Exp['b1Flx']
array([ 1.20660000e+15, 1.65202000e+16, 7.47956000e+16,
1.62709000e+17, 2.74814000e+17, 4.22295000e+17,
7.04931000e+17, 9.70795000e+17, 9.11899000e+17,
9.33758000e+17, 7.23255000e+17, 5.00291000e+17,
3.16644000e+17, 3.52049000e+17, 1.62308000e+17,
6.68674000e+16, 4.47932000e+16, 1.23599000e+16,
3.51299000e+16, 1.46504000e+16, 4.38516000e+15,
7.96971000e+14, 3.54233000e+14, 2.11013000e+13])
Data that does not contain the prefix INF_ or B1_ is stored
under the gc and gcUnc fields.
Criticality, kinetic, and other variables are stored under this field.
>>> univ3101.gc.keys()
dict_keys(['cmmTranspxs', 'cmmTranspxsX', 'cmmTranspxsY', 'cmmTranspxsZ',
'cmmDiffcoef', 'cmmDiffcoefX', 'cmmDiffcoefY', 'cmmDiffcoefZ', 'betaEff',
'lambda'])
>>> univ3101.gc['betaEff']
array([ 3.04272000e-03, 8.93131000e-05, 6.59324000e-04,
5.62858000e-04, 1.04108000e-03, 5.67326000e-04,
1.22822000e-04])
Macro- and micro- group structures are stored directly on the universe in MeV as they appear in Serpent output files. This means that the macro-group structure is in order of descending energy, while micro-group are in order of increasing energy:
>>> univ3101.groups
array([ 1.00000000e+37, 1.00000000e+01, 6.06530000e+00,
3.67880000e+00, 2.23130000e+00, 1.35340000e+00,
8.20850000e-01, 4.97870000e-01, 3.01970000e-01,
1.83160000e-01, 1.11090000e-01, 6.73800000e-02,
4.08680000e-02, 2.47880000e-02, 1.50340000e-02,
9.11880000e-03, 5.53090000e-03, 3.35460000e-03,
2.03470000e-03, 1.23410000e-03, 7.48520000e-04,
4.54000000e-04, 3.12030000e-04, 1.48940000e-04,
0.00000000e+00])
>>> univ3101.microGroups[:5:]
array([ 1.00000000e-10, 1.48940000e-04, 1.65250000e-04,
1.81560000e-04, 1.97870000e-04])
Plotting universes¶
HomogUniv objects can plot group constants using their
plot()
method. This method has a range of formatting options, with defaults
corresponding to plotting macroscopic cross sections. This is manifested
in the default y axis label, but can be easily adjusted.
>>> univ3101.plot(['infAbs', 'b1Abs']);
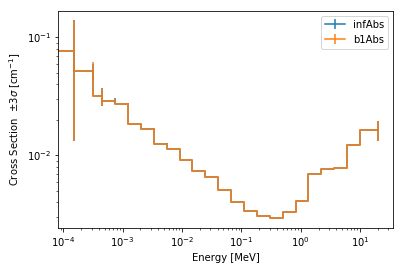
Macroscopic and microscopic quantities, such as micro-group flux, can be plotted on the same figure.
Note
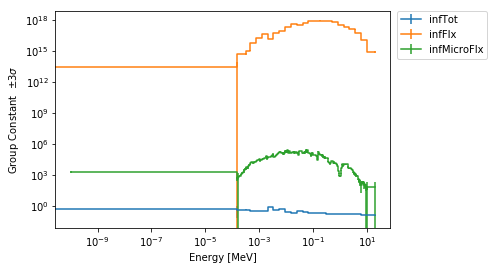
The units and presentation of the micro- and macro-group fluxes are dissimilar, and the units do not agree with that of the assumed group constants. This will adjust the default y-label, as demonstrated below.
>>> univ3101.plot(['infTot', 'infFlx', 'infMicroFlx'], legend='right');
For plotting data from multiple universes, pass the returned
matplotlib.axes.Axes object, on which the plot was drawn,
into the plot method for the next
universe. The labelFmt argument can be used to differentiate between
plotted data. The following strings are replaced when creating the
labels:
String |
Replaced value |
|---|---|
|
Name of variable plotted |
|
Name of this universe |
|
Value of burnup in MWd/kgU |
|
Value of burnup in days |
|
Burnup index |
These can be used in conjunction with the \(\LaTeX\) rendering system .
>>> fmt = r"Universe {u} - $\Sigma_{abs}^\infty$"
>>> ax = univ3101.plot('infFiss', labelFmt=fmt)
>>> univ3102.plot('infFiss', ax=ax, labelFmt=fmt, legend='above', ncol=2);
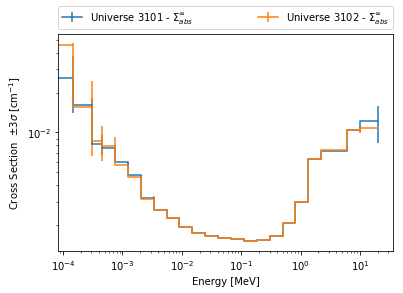
User Defined Settings¶
The user is able to filter the required information by using the
serpentTools.settings.rc settings object.
A detailed description on how to use the settings can be found on:
Default Settings.
>>> from serpentTools.settings import rc
>>> rc.keys()
dict_keys(['branching.areUncsPresent', 'branching.intVariables',
'branching.floatVariables', 'depletion.metadataKeys',
'depletion.materialVariables', 'depletion.materials', 'depletion.processTotal',
'detector.names', 'verbosity', 'sampler.allExist', 'sampler.freeAll',
'sampler.raiseErrors', 'sampler.skipPrecheck', 'serpentVersion', 'xs.getInfXS',
'xs.getB1XS', 'xs.reshapeScatter', 'xs.variableGroups', 'xs.variableExtras'])
The serpentTools.settings.rc object and various xs.* settings can be used to control the
ResultsReader. Specifically, these settings can be used to store only
specific pieces of information. Here, we will store the version of Serpent,
various cross sections, eigenvalues, and burnup data:
>>> rc['xs.variableGroups'] = ['versions', 'xs', 'eig', 'burnup-coeff']
Furthermore, we instruct the read to no read critical spectrum cross sections:
>>> rc['xs.getB1XS'] = False
>>> resFilt = serpentTools.readDataFile(resFile)
>>> resFilt.metadata.keys()
dict_keys(['version', 'compileDate', 'debug', 'title', 'confidentialData',
'inputFileName', 'workingDirectory', 'hostname', 'cpuType', 'cpuMhz',
'startDate', 'completeDate'])
>>> resFilt.resdata.keys()
dict_keys(['burnMaterials', 'burnMode', 'burnStep', 'burnup', 'burnDays',
'nubar', 'anaKeff', 'impKeff', 'colKeff', 'absKeff', 'absKinf', 'geomAlbedo'])
>>> univ0Filt = resFilt.getUniv('0', burnup=0.0, index=0, timeDays=0.0)
>>> univ0Filt.infExp.keys()
dict_keys(['infCapt', 'infAbs', 'infFiss', 'infNsf', 'infNubar', 'infKappa',
'infInvv', 'infScatt0', 'infScatt1', 'infScatt2', 'infScatt3', 'infScatt4',
'infScatt5', 'infScatt6', 'infScatt7', 'infTranspxs', 'infDiffcoef',
'infRabsxs', 'infRemxs', 'infChit', 'infChip', 'infChid', 'infS0', 'infS1',
'infS2', 'infS3', 'infS4', 'infS5', 'infS6', 'infS7'])
>>> univ0Filt.b1Exp
{}
Conclusion¶
The ResultsReader is capable of reading and storing all the data
from the SERPENT _res.m file. Upon reading, the reader creates
custom HomogUniv objects that are responsible for storing the universe
related data. In addition, metadata and resdata are stored on the reader.
These objects also have a handy getUniv() method for
quick analysis of results corresponding to a specific universe and time point.
Use of the serpentTools.settings.rc settings control object allows
increased control over the data selected from the output file.
References¶
J. Leppanen, M. Pusa, T. Viitanen, V. Valtavirta, and T. Kaltiaisenaho. “The Serpent Monte Carlo code: Status, development and applications in 2013.” Ann. Nucl. Energy, 82 (2015) 142-150